正则化与优化算法

Echo in Beijing

2020-09-02

# L1、L2 正则化

正则化的来源可以从两个角度考虑：

带约束条件的优化求解（拉格朗日乘子法）
贝叶斯学派的：最大后验概率

L1 正则可以通过假设权重 w 的先验为 Laplace 分布，由 MAP 导出。 L2 正则可以通过假设权重 w 的先验为 Gaussian 分布，由 MAP 导出。

总的来讲，L1 比 L2 更容易获得 sparse 的 w，L2 比 L1 更容易获得 smooth 的 w。

正则化起作用的原因：

使得网络中有用的节点变得更少
激活函数在 0 附近趋于线性，而线性的网络很难过拟合

参考 1，2。

# Dropout 正则化

给定 keep-prob，对每层的神经元输入 a 进行随机删除，使得训练过程中使用更小的网络。

# 假设对第三层神经网络进行 Inverted Dropout 操作
keep_prob = 0.8
d3 = np.random.rand(a3.shape[0], a3.shape[1]) < keep_prob
a3 = np.multipy(a3, d3) # a3 *= d3, element-wise
# 缩放 a 以保证 z 的期望不变 (z[4] = w[4] · a[3] + b[4])
a3 /= keep_prob

1
2
3
4
5
6

注意在随机删除神经元之后，为了保证下一层 z 的期望稳定，需要对本层 a 进行放缩，这也可以使得测试阶段变得简单，测试阶段的时候就不需要使用 Dropout 了，这也是 Inverted Dropout 成功替代原始的 Dropout 的原因。

注意，由于每层的参数量有差异，因此过拟合的可能性也不同，因此可以在不同的层设置不用的 keep-prob，参数多的层设置较小的 keep-prob。

其起作用的原因是：

每次迭代都使用更小的网络
由于不能依赖任何一个特征，因此将权重扩散，这就会收缩权重，像 L2 一样

计算机视觉的人会使用地更多一些，因为数据集一般比较小，很容易过拟合。但缺点是没有 well-defined 的损失函数来观测训练进度。

# 其他正则化方法

正则化的目的就是避免过拟合，因此也可以把以下避免过拟合的方法称为正则化：

data augmentation：图片翻转，数字扭曲等
early-stopping：用验证集的表现决定何时停止训练模型优于 L2 的一点是不需要尝试很多的 $\lambda$ ，但坏处是通常目标函数优化地不够好

# BN

在深层网络训练的过程中，由于网络中参数变化而引起内部节点数据分布发生变化的过程被称为 Internal Covariate Shift。

这会使得

顶层网络需要不断调整来适应输入数据分布的变化，导致网络学习速率的下降。
网络的训练过程容易陷入梯度饱和区（这与使用饱和激活函数 Sigmoid、Tanh 有相应的关系），减缓网络收敛速度。此时可以通过使用非线性饱和函数，比如 Relu，或者使得数据分布保持在非饱和区，这就是 BN 的思路。

ICS 产生的主要原因是每一层输入数据分布的改变，因此可以通过固定这个分布来减缓 ICS 问题，最简单的方式就是白化，但是白化存在两个问题：（1）计算成本太高（训练过程中对每一层的输入都要 PCA），（2）改变了网络中每一层的分布，因而削弱了网络原本的表达能力。

而 BN 的提出正是为了解决这两个问题，对于具体的算法，这里有很直观的解释。其奏效的原因是：

归一化到 0 均值、1 方差，可以加速学习
通过减弱 ICS 削弱了前层参数的作用与后层参数的作用之间的联系（解耦？），它使得网络每层都可以自己学习，稍稍独立于其他层，这有助于加速整个网络的学习
不同 mini-batch 的均值方差往往不同，相当于往每个隐藏层的激活值上增加了噪音，具有轻微的正则化效果

总的来说，BN 是归一化隐藏单元激活值并加速学习的方式。

当测试的时候，通常是单个样本的计算，因此不会涉及到均值和方差的概念，这是一般采用训练过程中所有 batch 的指数加权平均来粗略估算测试时的均值和方差。

# 指数加权平均

指数加权平均表达为

$v_t = \beta v_{t-1} + (1 - \beta) \theta_t$

其中， $\theta_t$ 为当次的值， $v_t$ 为累积到第 t 次的指数加权平均值。

一般情况下， $v_t$ 在一开始（ $t$ 较小的时候）会表现地很差，因此需要对其进行偏差修正。

修正的方式为，在计算的时候公式仍然不变，但是在使用的时候不用 $v_t$ ，而是用 $\frac{v_t}{1 - \beta^t}$ 。可以发现，当 $t$ 很大的时候，分母会接近 1，因此修正后的结果会接近于原始结果 $v_t$ 。

# 优化算法

梯度下降是使用最广泛的优化方法，但由于其过程的波动性较大，使得优化时不能使用较大的学习率（避免优化偏离函数范围），从而降低了学习的速度。

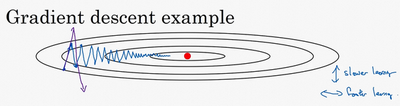
如图所示，通常我们希望他的在纵轴上的摆动幅度小一些，而在横轴上加速学习。因而产生了很多变种。

# Momentum

动量（Momentum）梯度下降法就是对梯度使用了指数加权平均，在计算好 $dW, db$ 之后，不是直接用他进行更新，而是使用如下公式更新权重。

$\begin{aligned} & v_{dW} = \beta_1 v_{dW} + (1 - \beta_1) dW \\ & v_{db} = \beta_1 v_{db} + (1 - \beta_1) db \\ & W = W - \alpha v_{dW}, b = b - \alpha v_{db}\\ \end{aligned}$

且在深度学习实践中， $\beta = 0.9$ 通常是一个很鲁棒的值。

可以发现，在纵轴上（波动的方向），由于其正负相间，所以当求了平均之后会接近于零，波动会变小，而在与波动方向垂直的横轴上，其学习速度仍然较大。

# RMSprop

RMSprop 则是对梯度的平方使用了指数加权平均，该方法也可以加速梯度下降，其公式为

$\begin{aligned} & S_{dW} = \beta_2 S_{dW} + (1 - \beta_2) (dW)^2 \\ & S_{db} = \beta_2 S_{db} + (1 - \beta_2) (db)^2 \\ & W = W - \alpha \frac{dW}{\sqrt{S_{dW}}}, b = b - \alpha \frac{db}{\sqrt{S_{db}}}\\ \end{aligned}$

假设 $b$ 所在的方向为纵轴， $W$ 所在的方向为横轴，由于微分在纵轴的波动大一些，导致 $(db)^2$ 会更大，因此 $S_{db}$ 会大一些，因而 $db$ 会被一个较大的数相除，这样就能消除摆动，而水平方向的更新则被较小的数相除。

此时就可以使用一个较大的学习率加快学习，但不会在纵轴方向上偏离函数范围。

通常会给平方根内的数加一个很小的 $\epsilon = 10^{-8}$ ，确保算法不会除零。

# Adam

Adam 全称为 Adaptive Moment Estimation，它就是 Momentum 和 RMSprop 的有机结合。

先分别对 $dW, db$ 做 Momentum 和 RMSprop，求得 $v_{dW}, v_{db}, S_{dW}, S_{db}$ ，然后计算偏差修正，最后用修正后的结果更新权重

$W = W - \alpha \frac{v_{dW}^{corrected}}{\sqrt{S_{dW}^{corrected} + \epsilon}}, b = b - \alpha \frac{v_{db}^{corrected}}{\sqrt{S_{db}^{corrected} + \epsilon}}$

至于超参数，通常设置 $\beta_1 = 0.9, \beta_2 = 0.999$ ，其中 $\beta_1$ 用于计算 $dW$ 指数移动加权平均，叫做一阶矩， $\beta_2$ 用于计算 $(dW)^2$ 的指数移动加权平均，叫做二阶矩，这也是 Adam 名字的由来。