聚类算法

# 基于距离

K-means 是基于距离的聚类方法的代表，这类方法的聚类结果都是球状的簇，当数据中存在非球状结构时，其效果并不好。

# K-means 适用条件

但 K-means 算法简单有效，其适用条件为：

• 空间中存在距离度量 <a, b>，且满足 <a, b> = <b, a>
• 存在求中心点的算法

比如瑞士卷图就不满足这样的条件，因此不适合使用 K-means 算法。

# K-means 改进算法

针对 K-means 算法有很多改进，比如 优化初始化类中心的 K-means ++，动态调整类个数的 ISODATA，避免陷入局部最优的二分 K-means，解决海量数据聚类的 Mini-Batch K-means 等。

这里简单说一下 K-means ++。该算法改进了 K-means 算法的初始化类中心的过程，使得一开始的类中心能够尽可能地分散。具体方法是：

• 计算每一个样本点 $x$ 到已有的类中心的最短距离 $D(x)$

• 计算每个样本点被选为下一个类中心的概率 $\frac{D(x)^2}{\sum_{x \in X} D(x)^2}$

• 按样本顺序求概率累加和，按照轮盘法选择出下一个类中心

# 基于密度

与基于距离的聚类算法不同的是，基于密度的聚类算法可以发现任意形状的聚类，DBSCAN 便是这类方法的一个代表。

# DBSCAN 算法

DBSCAN 算法的基本思想是寻找被低密度区域分离的高密度区域，作为一个“簇”。其中“簇”的定义为：由密度可达关系导出的最大密度相连样本的集合。

# DBSCAN 与 K-means 对比

	K-means	DBSCAN
数据集	只适用于凸样本集，聚类结果为球状簇	对样本集无要求，可以发现任意形状的簇，但当聚类密度不均匀时，聚类质量较差
初始化	需要预先声明聚类个数，且初始值对结果影响较大	不需要预先声明聚类个数，聚类结果没有偏倚
异常值	对异常值较为敏感	对异常值不敏感
海量数据	考虑 mini-batch K-means	建立 KD 树搜索最近邻

# 谱聚类

谱聚类是广泛使用的聚类算法，比起传统的 K-means，谱聚类对数据分布的适应性更强，聚类效果也更优秀，同时计算量也小很多，实现起来也不复杂。

谱聚类的思想是将原始样本点看作图中的节点，用顶点间的相似度度量作为边的权重，构造相似度矩阵，从而将聚类问题转化为图划分问题。而基于图论的最优划分准则就是使划分得到的子图内部相似度最大，子图之间相似度最小。

其实说白了就是构建相似矩阵，子图划分（用 Laplace 矩阵求解特征向量），聚类划分数据簇，而这三部分别最常用的是基于高斯核的全连接方式，基于权重的 Ncut 切图以及 K-means 聚类。

但是谱聚类非常依赖于相似矩阵的构建，因此不同的距离度量对最终的聚类效果影响很大。

参考 1。

# 模型聚类

代表为 GMM 模型，它是一个生成模型，该模型试图找到多为高斯模型概率分布的混合表示，从而拟合出任意形状的分布。

它使用 EM 算法进行迭代，而且给出的聚类结果是软聚类，即每一个样本只给出属于每一类的概率，同时在模型运行结束后，还可以用于生成新的样本。这些特性使得 GMM 在风控领域非常受欢迎。

# 层次聚类

层次聚类分为自顶向下和自底向上两种方式，也叫分裂和凝聚。自顶向下是将单个连通网络不断划分，直到每个分支只有单个节点为止，自底向上则相反。

其分裂（凝聚）依据的差异产生了不同的算法，层次分裂的代表是用于社区发现的 GN 算法，而层次凝聚的代表是 AGNES 算法。

可以看到，层次聚类的局限之处在于较高的时间复杂度，因为每更新一步，所有的簇都需要重新计算度量。

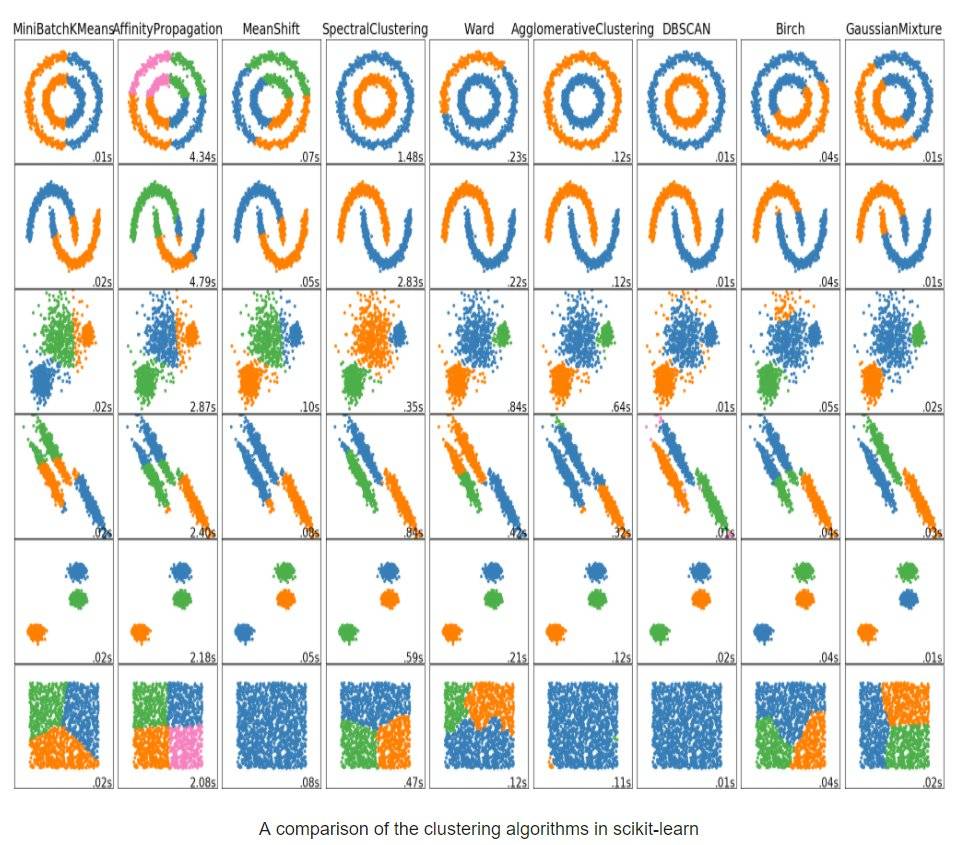
最后，附上一张各种聚类的效果图 👏。