深度学习问答

Echo in Beijing

2020-09-12

深度学习

# Q1：如何调试超参数？

一般有两种方式：GridSearch 和 RandomSearch。

在选点个数一致的情况下，RandomSearch 会测试更多的超参数，比如对两个超参数选择 25 个点，对于第一个超参数 GridSearch 只能测试 5 个值，而 RandomSearch 也许可以测试 25 个值，这显然更高效，因此个人倾向于 RandomSearch。

# Q2：如何给超参数选择合适的范围？

不同的超参数选择方式不同，但一般分为两种：线性随机选择和指数随机选择。

线性随机选择就是在指定范围内线性生成随机数，写法如下

# 在 [a, b) 之间线性选择，比如网络层数范围为[2, 5)
para = np.random.rand() * (b - a) + a

1
2

这种方式一般适用于神经网络的层数，每层的隐藏单元数等参数。

指数随机选择就是对指定范围求对数，然后生成随机数，再指数映射回去，写法如下

# 对范围 [10^a, 10^b) 取对数，比如学习率范围为 [0.001, 1)
a, b = np.log10(10^a), np.log10(10^b)
# 生成 [a, b) 之间的随机数
r = np.random.rand() * (b - a) + a
# 指数映射回去
para = 10 ^ r

1
2
3
4
5
6

这种方式一般适用于学习率，指数加权平均中 $1 - \beta$ 等参数。

# Q3：梯度爆炸/消失是如何产生的？怎么解决？

# 如何产生？

在以梯度下降算法进行反向传播的时候，会运用链式求导法则进行更新梯度的计算，而在链式求导的时候就会出现

\frac{\part \mathcal{L}}{\part w_i^{[2]}} = \frac{\part \mathcal{L}}{\part a_i^{[4]}} \cdot \frac{\part a_i^{[4]}}{\part a_i^{[3]}} \cdot \frac{\part a_i^{[3]}}{\part a_i^{[2]}} \cdot \frac{\part a_i^{[2]}}{\part w_i^{[2]}}

这里 $a_i^{[4]} = \hat{y_i}$ ，而 $ \frac{\part a_i^{[3]}}{\part a_i^{[2]}} = \sigma'(z_i^{[3]})w_i^{[3]}$，可以看到，导数里存在两项：(1) 激活函数的导数，(2) 权重。

当层数累积到一层程度的时候，这两项中的任何一项都会指数变化。比如神经网络有 20 层，

权重：当权重大于 1 的时候，假设每一层的权重都为 1.5，那么 1.5^20 会是一个很大的数，就会产生梯度爆炸的现象；反之当梯度小于 1，假设为 0.5 的，就会产生梯度消失的现象
激活函数的导数：当激活函数进入梯度饱和区以后，即导数趋于 0 的时候，就会产生梯度消失的问题

总的来说，产生梯度爆炸/消失的因素有如下三点：

链式求导
权重
激活函数的导数

# 如何解决？

既然知道了原因，那么我们可以分别从不同的角度去解决这个问题。

分层训练再 fine-tuning：避免链式求导的累积效应
梯度裁剪：当梯度达到某个阈值之后对其进行裁剪强制限制在某个范围内，防止梯度爆炸
正则化方法：避免了参数过大梯度爆炸，也避免了激活函数进入饱和区
选择激活函数：Relu 类的激活函数在输入大于 0 的时候梯度恒为 1，避免了激活函数进入梯度饱和区
Batch-Norm：对每一层的输出进行正则化避免了激活函数进入饱和区，也使得权重不会过分依赖于某个特征（不会过大）
ResNet 残差结构：shortcut 使得有效网络变短，在一定程度上缓解了梯度爆炸/消失问题

# Q4：神经网络权重的初始化。

不要用全零，会导致神经网络同意隐藏层的所有神经元做同样的计算，因而无论如何使用梯度下降优化都无济于事。应该使用随机初始化，且初始化为小值（例如 0.01）。

# Q5：ResNet 起作用的原因。

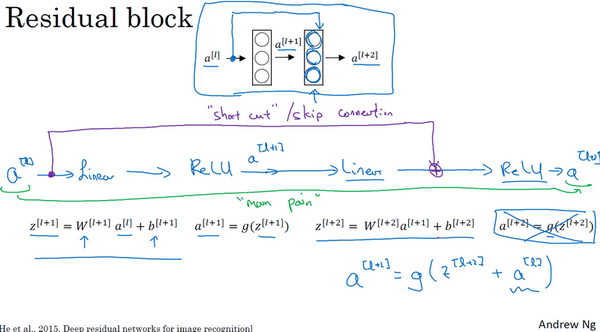
ResNet 使用跳跃连接，使得 $a^{[l+2]} = g(z^{[l+2]} + a^{[l]})$ ，其中激活函数 $g$ 为 ReLU， $z^{[l+2]} = W^{[l+2]}a^{[l+1]} + b^{[l+2]}$ ，当存在正则项或者权重衰减的时候， $W^{[l+2]}, b^{[l+2]}$ 很容易变成 0，这就使得 $a^{[l+2]} = g(a^{[l]}) = a^{[l]}$ ，即让残差块学习这个恒等函数，对于神经网络而言它并不难。

而这些残差块能够很容易地学习恒等函数也就保证了网络的性能不会降低，此外，如果这些残差块能够学到一些有用信息，那就可能比学习恒等函数表现得更好，因此残差网络可以提升网络性能。

# Q6：TCN 是什么？

TCN 全称 Temporal Convolution Networks，相比于 RNN 类的网络，它可以用更少的内存、更快的速度捕捉更长的时间序列。

TCN 使用 Dilated Convolution 来扩大 Reception Field，使用残差结构来避免梯度问题和加深网络结构，使得它能够捕捉更长的时间序列。同时其非序列化的结构优势（RNN 为序列结构）使得网络可以大规模并行处理。

但 TCN 也有缺点：

没有 RNN 那样的“无限记忆”单元（特指隐状态），预测的时候只需要一个隐藏状态和当前时间的输入，TCN 预测时需要输入完整的序列。
由于不同问题的历史信息量不一致，因此 TCN 的迁移能力不好。

# Q7：`1x1` 卷积有什么作用？

1x1 卷积的作用有如下两点：

降维（或升维）：卷积核的大小一般为 [kernel_size, kernel_size, in_channels, out_channels]，于是我们就可以使 out_channels < in_channels 来降维。
增加非线性：多一层卷积自然会增加非线性（依靠非线性激活函数），但是用 1x1 的好处是什么呢？因为 1x1 的卷积核可以保持 feature map 的尺寸不变，也就是不损失分辨率。